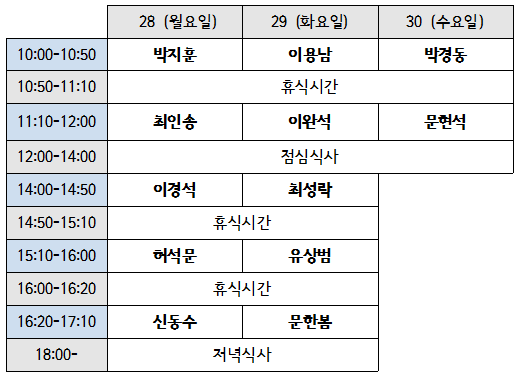
박지훈 (POSTECH/IBS-CGP)

- Title: Automorphisms of the complements of hypersurfaces

- Abstract: We discuss the automorphism groups of the complements of hypersurfaces in (weighted) projective spaces.

최인송 (건국대학교)

- Title: Bisecant curves on ruled surfaces

- Abstract: We discuss the existence of certain bisecant curves on ruled surfaces over a curve of higher genus. It is related to the degree of stability of the associated rank 2 bundles. This is a joint work with Youngook Choi, Seonja Kim, and Euisung Park.

이경석 (IBS-CGP)

- Title: Ulrich bundles on some Fano manifolds

- Abstract: Ulrich bundles are special vector bundles on algebraic varieties which draw lots of attention in these days. In the first part of this talk, I will review basic results and recent developments about Ulrich bundles. Then I will discuss the existence and moduli problem of Ulrich bundles on some Fano manifolds using Borel-Weil-Bott theorem, Serre correspondece and derived categories of coherent sheaves. This talk is based on joint works with Yonghwa Cho, Yeongrak Kim and Kyeong-Dong Park.

허석문 (성균관대학교)

- Title: wildness of K3 surfaces

- Abstract: In representation theory of quivers, due to Gabriel's theorem, we may classify connected quivers as finite, tame or wild type in terms of the families of indecomposable modules over the associated path algebras. Motivated by this trichotomy classification, a similar classification has been tried on projective schemes to understand their complexity in terms of the families of arithmetically Cohen-Macaulay (aCM for short) sheaves. In this talk, we will present our recent result to show that any integral surface with trivial canonical sheaf and zero irregularity supports arbitrarily large dimensional families of indecomposable aCM vector bundles, which concludes that the prescribed surfaces are wild. 

This is a joint work with E. Ballico and J. Pons-Llopis. 

신동수 (충남대학교)

- Title: Smoothly embedded rational homology balls and Mori sequences of antiflips

- Abstract: I would like to detect a rational homology ball smoothly embedded in a given smooth 4-manifold, where a rational homology ball is a smooth 4-manifold  with boundary whose higher cohomology with rational coefficient vanish. To this purely topological problem, I will apply the semi-stable minimal model program for 3-folds in algebraic geometry; explicitly, the universal family of antiflips constructed by [Mori 2002] and [Hacking-Tevelev- Urzúa 2016]. As a result, we show that there are infinitely many pairs of disjoint rational homology balls in regular neighborhoods of `almost all' linear chains of negative rational curves. If time permits, I will discuss a possible application and further research topics on explaining semi-stable antiflips in MMP on the level of Kirby calculus or two-bridge knot diagrams in topology. This is a joint work with Heesang Park and Giancarlo Urzúa.

이용남 (KAIST)

- Title: On rational maps from the product of two general curves

- Abstract:

이완석 (부경대학교)

- Title: Decomposition of Betti tables of Curves on rational normal surface scrolls

- Abstract:

최성락 (연세대학교)

- Title: A product formula for volumes of divisors via Okounkov bodies

- Abstract: We generalize Kawamata's product formula for volumes of canonical divisors to arbitrary divisors using the Okounkov bodies.

유상범 (UNIST)

- Title: Finite generation of the algebra of type A conformal blocks over a curve

- Abstract:

문한봄 (IAS)

- Title: Finite generation of the algebra of type A conformal blocks over a curve - Part 2

- Abstract: This is a supplement of the previous talk of Dr. Yoo on the finite generation of the algebra of conformal blocks. I will review a classical analogue of conformal blocks and introduce conformal blocks as quantum generalization of them. Then I will explain a consequence and an application of the finite generation. 

박경동 (IBS-CGP)

- Title: Liouville property of smooth horospherical varieties of Hermitian symmetric type

- Abstract: A horospherical variety is a complex normal algebraic variety such that a connected reductive algebraic group acts with an open orbit isomorphic to a torus bundle over a rational homogeneous variety. Horospherical varieties form a large class of algebraic varieties containing toric varieties and rational homogeneous varieties, and can be described by colored fans. In this talk, I will explain that smooth horospherical varieties of Hermitian symmetric type have Liouville property, that is, every local vector field preserving the cone structure associated to the variety of minimal rational tangents can be extended to a global vector field on a Zariski open subset.

문현석 (KAIST)

- Title: REAL RANK GEOMETRY OF QUADRICS

- Abstract: The real Waring rank is the least number of real linear forms whose sums of d-th power is same as the given form. We study the real ternary and quaternary forms whose real rank equals the generic complex rank, and we characterize the semialgebraic set of sums of powers with that rank.

For quadrics, with any number of variables, there is only one typical real rank which is same as the generic complex rank. So we should focus on the semialgebraic set of sums of powers, that represents what kind of real linear forms actually give the real rank decomposition. The algebraic boundary is related to the hyperdeterminant. For ternary case, the algebraic boundary is smooth. But for quaternary case, it is singular and there are interesting geometric and algebraic meaning in these singular parts. In this talk, we present these structures and give some expectations for more variable cases.

This is a joint work with Mateusz Michalek.