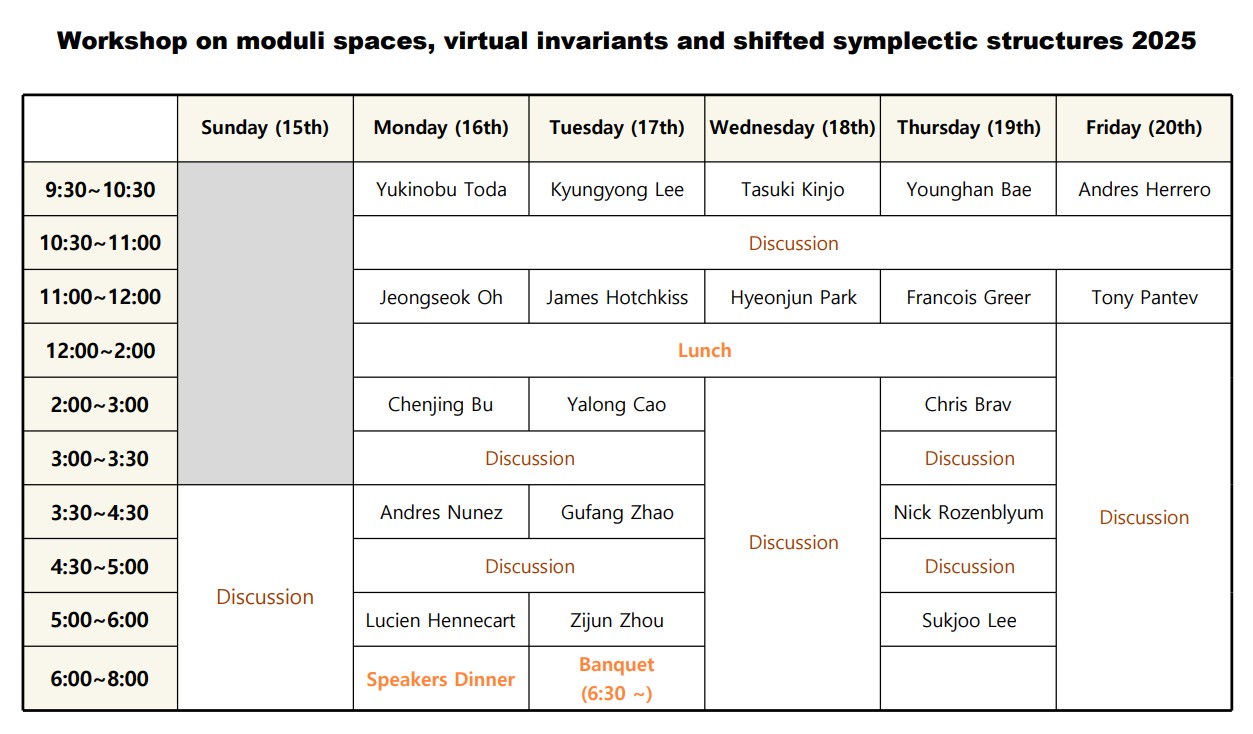
| Program | Home > Program |
Yukinobu Toda (IPMU)
Title: Dolbeault geometric Langlands conjecture and quasi-BPS categories
Abstract: In this talk, I will introduce the notion of limit categories for cotangent stacks of smooth stacks as an effective version of classical limits of the categories of D-modules on them. Using the notion of limit categories, I will propose a precise and tractable formulation of the Dolbeault geometric Langlands conjecture, proposed by Donagi–Pantev as the classical limit of the geometric Langlands correspondence. It states an equivalence between the derived categories of coherent sheaves on moduli stacks of semistable G-Higgs bundles for a reductive group G and the limit category of moduli stacks of G^L-Higgs bundles without a stability condition. I will show the existence of a semiorthogonal decomposition of the limit category into quasi-BPS categories, which (when G=GL_r) categorify BPS invariants on a non-compact Calabi–Yau 3-fold playing an important role in Donaldson-Thomas theory. This semiorthogonal decomposition is interpreted as a Langlands dual to the semiorthogonal decomposition for moduli stacks of semistable Higgs bundles, obtained in our earlier work as a categorical analogue of PBW theorem in cohomological DT theory. It in particular yields a conjectural equivalence between quasi-BPS categories, which gives a categorical version of Hausel-Thaddeus mirror symmetry for Higgs bundles (for any G), This is a joint work in progress with Tudor Pădurariu.
Jeongseok Oh (Seoul National University)
Title: A pullback between sheaves on log Calabi-Yau 4-folds
Abstract: Given a section of a bundle with quadratic form, we construct a specialisation map between K-groups of matrix factorisations of the quadratic function from the space to the normal cone of the zero locus. When the section is isotropic, the quadratic function becomes zero and the construction recovers usual specialisation map in Fulton-MacPherson's intersection theory.
When a log Calabi-Yau 4-fold (X,D) is given, we apply the construction to define a pullback from sheaves on D to ones on X after assuming the space of sheaves on D is a critical locus globally. For a Calabi-Yau 4-fold X, we artificially define "the space of sheaves on D" to be a point so that its structure sheaf pulls back to the virtual structure sheaf of the space of sheaves on X.
This is a joint work in progress with Dongwook Choa and Richard Thomas.
Chenjing Bu (University of Oxford)
Title: The component lattice
Abstract: I introduce the component lattice, which is a combinatorial object assigned to any algebraic stack. It is a globalization of the coweight lattice and the Weyl group of an algebraic group. This is motivated by the problem of generalizing enumerative geometry from linear cases, that is moduli of objects in linear categories, to general non-linear stacks, and these applications will be discussed by my collaborators in later talks. This talk is based on a joint work with Daniel Halpern-Leistner, Andrés Ibáñez Núñez, and Tasuki Kinjo.
Andrés Ibáñez Núñez (Columbia University)
Title: Intrinsic Donaldson–Thomas Theory
Abstract: The language of the component lattice, introduced in Chenjing Bu’s talk, allows us to define a so-called epsilon motive on general algebraic stacks, generalizing a construction of Joyce when the stack parametrizes objects in an abelian category. The epsilon motive satisfies a no-pole property and thus it yields a notion of Euler characteristic for general Artin stacks, and of Donaldson-Thomas invariant for (-1)-shifted symplectic stacks. Our language makes it possible to give a simple proof of the no-pole property, substantially simplifying the classical theory in the abelian category setting.
The epsilon motive depends on a stability measure on the stack, a certain kind of stability data. Stability measures are naturally points of a unipotent algebraic group. Wall-crossing formulas when we vary the stability measure can be expressed in terms of the group law.
This talk is based on joint work with Chenjing Bu and Tasuki Kinjo.
Lucien Hennecart (CNRS)
Title: Cohomological Mackey formula for representations of reductive groups
Abstract: I will describe the construction of induction and restriction morphisms on the critical cohomology associated with a function on a representation of a reductive group. The induction morphism plays a key role in obtaining a cohomological integrality decomposition, which is a decomposition into finite-dimensional pieces with enumerative significance. After discussing this decomposition and its geometric meaning, I will present a cohomological version of the Mackey formula that relates the induction and restriction operations.
Kyungyong Lee (University of Alabama)
Title: Scattering diagrams, relative Gromov-Witten invariants, and moduli spaces of framed stable representations
Abstract: This is a joint work with Amanda Burcroff and Lang Mou. We discover a manifestly positive formula for any wall-function in a rank-2 generalized cluster scattering diagram. Our formula yields explicit expressions for relative Gromov-Witten invariants on weighted projective planes and the Euler characteristics of moduli spaces of framed stable representations on complete bipartite quivers. Finally, by leveraging the rank-2 positivity, we show that any higher-rank generalized cluster scattering diagram has positive wall-functions, which leads to a proof of the positivity of the Laurent phenomenon and the strong positivity of Chekhov-Shapiro's generalized cluster algebras.
James Hotchkiss (Columbia University)
Title: The topological period-index conjecture
Abstract: The period-index problem is an elementary question about central simple algebras over a field, originating in the calculation of the Brauer groups of number fields from the early part of the twentieth century. The problem is widely open. I will explain an analogue of the problem (and its solution) for topological spaces, and the connection with the integral Hodge conjecture for certain CY3 categories.
Yalong Cao (Morningside Center of Mathematics)
Title: Critical pullback in K-theory
Abstract: Given a (-1)-shifted Lagrangian L on a derived critical locus Crit(f), under fairly general hypothesis, we construct a natural pullback map from the critical K-theory of f to the Grothendieck group of coherent sheaves on L, and show it satisfies natural functorial properties. Applied to the case of quasimaps to critical loci, it allows us to define quantum critical K-theory. Joint work with Yukinobu Toda and Gufang Zhao.
Gufang Zhao (University of Melbourne)
Title: Line Operators from a 3-Calabi–Yau Category
Abstract: Starting from a symmetric 3-Calabi–Yau category equipped with additional structure, we construct a triangulated monoidal category with a weak braiding. When the 3-Calabi–Yau category arises from the root datum of a simple algebraic group, we compare the resulting category with the equivariant derived category of coherent sheaves on the affine Grassmannian—namely, coherent sheaves on the Hecke stack.
We further examine monoidal categories associated to an algebraic group together with a representation, known as categorified Coulomb branches, or equivalently, categories of line operators in 4d mathcal{N}=2 gauge theories. Finally, we discuss the abelian heart of the perverse t-structure on coherent sheaves and its cluster structure as studied by Cautis and Williams.
This talk is based on ongoing joint work with Fujita, Yang, and Soibelman.
Zijun Zhou(Shanghai Jiao Tong University)
Title: Coulomb Branch and Enumerative Geometry
Abstract: Coulomb branches of 3d N=4 theories and their quantizations, originated in physics and later developed by Braverman-Finkelberg-Nakajima, provide new geometric ways of constructing alge bras and their representations. In this talk, I will discuss its connection to enumerative geometry, where representations of Coulomb branches are expected to show up in the moduli of quasimaps into Higgs branches (i.e. GIT quotients). Interesting enumerative invariants, such as I- functions/Okounkov’s vertex functions, quantum differential/difference modules, etc. can be described in terms of quantized Coulomb branch. In the case of holomorphic symplectic quotients , we also need to intro duce a virtual variant of the Coulomb branch, where the convolution product is modified by a virtual intersection. Applications include the invariance of quantum differential/difference equations under variation of GIT.
Tasuki Kinjo (RIMS)
Title: Lagrangian correspondence, cohomological Hall induction and decomposition theorem
Abstract: In the first half of the talk, I will introduce and motivate Joyce’s conjecture on the functoriality of cohomological Donaldson–Thomas invariants under Lagrangian correspondences. The proof of this conjecture will be explained in Park’s subsequent talk. I will also explain how this conjecture implies the construction of the cohomological Hall algebra for 3-Calabi–Yau categories and its generalization—the cohomological Hall induction for (−1)-shifted symplectic stacks—which was defined in my joint work with Pavel Safronov and Hyeonjun Park.
In the second half of the talk, I will discuss an application of cohomological Hall induction. I will explain how this structure together with the formalism of component lattices provide an explicit form of the decomposition theorem for the good moduli space morphisms for stacks satisfying certain symmetry assumptions. By combining this decomposition with the Atiyah–Bott recursion, we obtain a recursive formula for the intersection cohomology of the moduli space of semistable G-bundles on a Riemann surface. If time permits, I will describe how this formalism leads to a formulation of the topological mirror symmetry conjecture for the moduli stack of G-Higgs bundles, extending the Hausel–Thaddeus conjecture beyond type A groups. This part of the talk is based on joint work with Chenjing Bu, Ben Davison, Andrés Ibáñez Núñez, and Tudor Pădurariu.
Hyeonjun Park (KIAS)
Title: Lagrangian classes, Donaldson-Thomas theory, and gauged linear sigma models
Abstract: In this talk, I will explain the construction of Lagrangian classes for perverse sheaves in cohomological Donaldson-Thomas theory, following Tasuki Kinjo’s talk. The two key ingredients are a relative version of the DT perverse sheaves and a hyperbolic version of the dimensional reduction theorem. As a special case, we recover Borisov-Joyce/Oh-Thomas virtual classes in DT4 theory.
As applications, I will explain how to construct the following structures from the Lagrangian classes: (1) cohomological field theories for gauged linear sigma models, (2) relative Donaldson-Thomas invariants for Fano 4-folds with anti-canonical divisors, (3) refined surface counting invariants for Calabi-Yau 4-folds.
This is joint work in progress with Adeel Khan, Tasuki Kinjo, and Pavel Safronov.
Younghan Bae(University of Michigan)
Title: Intersection theory of Artin stacks and applications to stacks of bundles on moving curves
Abstract: In many moduli problems, the parameter space naturally takes the form of an Artin stack. Studying the intersection theory of such stacks raises several questions: which definition of Chow group to use, and which methods are available for computations?
In this talk, we first show that the natural cycle class map from Kresch's Chow group to Khan's Chow group is an isomorphism over integer coefficients. We then present a relative localization formula. As applications, we study: (i) Kontevich-type stable maps to a target X that is smooth and projective over BG, and (ii) the Hall product structure on the moduli stack of coherent sheaves over the moduli space of smooth curves. This is a joint work in progress with H. Park. The application to the Hall product is joint work in progress with W. Lim.
Francois Greer (Michigan State University)
Title: Elliptic-Elliptic Surfaces
Abstract: Consider the moduli space of elliptic surfaces of height 1 over an elliptic base curve. These surfaces have Kodaira dimension 1, but their middle Hodge structures are K3-type. The period map is generically finite onto an orthogonal Shimura variety. We will show that there is an algebraic correspondence between any such surface and an associated K3 surface. We propose a conjectural twisted Fourier-Mukai duality between pairs with the same associated K3. This is based on joint work with Yilong Zhang and Donu Arapura.
Chris Brav (Shanghai Institute for Mathematics and Interdisciplinary Science)
Title: Non-commutative calculus, connections, and loop spaces
Abstract: The Cartan calculus concerns vector fields on a smooth variety X acting on differential forms via Lie derivative and contraction, with Cartan's magic formula expressing the relation between the two actions: Lie derivative is the graded commutator of the de Rham differential with contraction. On a smooth variety, the magic formula can be checked in local coordinates, while for singular schemes (and more general prestacks) it is necessary to work with the tangent complex, where it is no longer feasible to give explicit local formulas. Interpreting the magic formula as giving Griffiths transversality for the Gauss-Manin connection of the universal infinitesimal deformation of X, we are able to construct a formula-free, chain level Cartan calculus using the tangent complex of a singular scheme, and to establish the compatibility of this calculus with the noncommutative calculus of Hochschild cochains acting on Hochschild chains. This is joint work with Nick Rozenblyum.
Nick Rozenblyum ( University of Toronto)
Title: Hamiltonian flows on moduli spaces
Abstract: A classical theorem of Goldman states that the states that a Lie algebra of loops on a Riemann surface acts by Hamiltonian vector fields on its character variety. I will describe a vast generalization of this fact: that a certain noncommutative period map for (relative) Calabi-Yau categories is Poisson. In addition to generalizing Goldman's theorem to higher dimensions, we obtain a number of other interesting examples including new constructions of integrable systems. This is joint work with Chris Brav.
Sukjoo Lee (IBS-CGP)
Title: Geometry of $xi$-parabolic Higgs bundles and relative spectral correspondence.
Abstract: Since Simpson’s introduction of the tame non-abelian Hodge correspondence, parabolic Higgs bundles have played a significant role in the study of moduli spaces and related areas. Among them, diagonally parabolic Higgs bundles—also known as $xi$-parabolic Higgs bundles—serve as fundamental building blocks for understanding the geometry of the moduli space of parabolic Higgs bundles. In this talk, I will give an overview of the geometry of $xi$-parabolic Higgs bundles and present a relative version of the spectral correspondence originally introduced by Chuang–Diaconescu–Donagi–Pantev. If time permits, I will also explain applications to the multiplicative Deligne–Simpson problem. This is joint work with Jiachoon Lee.
Andres Herrero (University of Pennsylvania)
Title: Decomposition theorem for the logarithmic Hitchin fibration
Abstract: This talk will focus on the intersection cohomology of the moduli space of semistable logarithmic G-Higgs bundles on a smooth curve, where G is a reductive group. I will explain a uniform description of the decomposition theorem for the corresponding Hitchin fibration, and how this can be used to understand the degree dependence of the intersection cohomology of the moduli space. This is based on joint work with Mark Andrea de Cataldo, Roberto Fringuelli and Mirko Mauri.
Tony Pantev (University of Pennsylvania)
Title: Birational and singularity invariants from nc Hodge theory
Abstract: I will explain how a natural amalgam of classical Hodge theory with the nc Hodge structures arising from Gromov-Witten theory gives rise to new additive invariants of smooth projective varieties called Hodge atoms. Combined with Iritani's blow-up formula, Hodge atoms provide obstructions to birational equivalence and novel invariants of singularities. I will discuss applications to classical rationality problems and singularity theory. This is a joint work with L.Katzarkov, M.Kontsevich, and T.Y.Yu.
