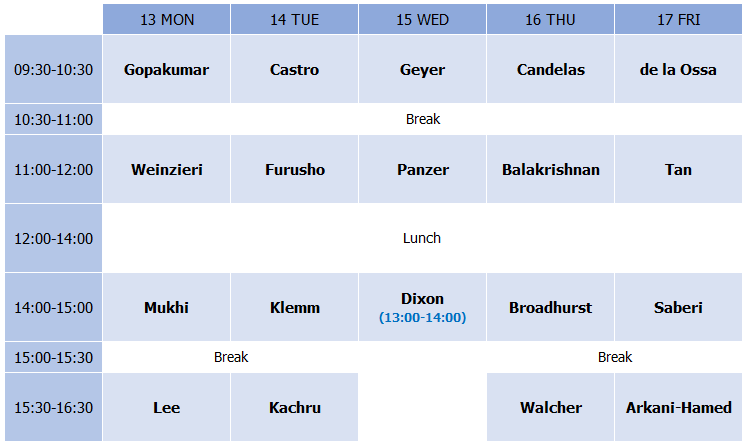
13  MON

◆ Rajesh Gopakumar (ICTS-TIFR, Bengaluru)

- Title: Arithmetic Gauge-String Duality

- Abstract: Gauge-String Duality has been one of the central themes of theoretical physics for the last decade.Yet the scope and underlying mechanism for these dualities is poorly understood. I will focus on the case of simple matrix integrals to illustrate a mechanism by which Feynman diagrams of a gauge theory can be glued up into closed string Riemann surfaces. The basic ingredient is the Strebel decomposition of the moduli space of Riemann surfaces. In the simple case of the Gaussian matrix integral the additional interesting feature is the natural way in which a special class of holomorphic maps called Belyi maps arise. This seems to indicate that arithmetic Riemann surfaces play a role in the dual string theory which we conjecture to be a topological closed string theory.

◆ Stefan Weinzierl (Mainz)

- Title: Elliptic curves in precision calculations in high-energy particle physics

- Abstract: Precision calculations in high-energy particle physics are based on Feynman integrals. We may ask what functions do we get if we compute Feynman integrals? There is a large class of Feynman integrals -- mostly related to massless theories --yielding multiple polylogarithms.
In this talk I will focus on the question "What comes beyond?”. It is well-known that starting at two-loops and with internal masses there are Feynman integrals which cannot be expressed in terms of multiple polylogarithms. These are relevant to precision physics with heavy particles at the LHC. I will review the current state of the art, discuss a class of Feynman integrals, which are associated to a single elliptic curve. These may be expressed as iterated integrals of modular forms or elliptic polylogarithms. I will also discuss more complicated Feynman integrals, where more than one elliptic curve occurs.

◆ Sunil Mukhi (IISER Pune)

- Title: Fermions on Replica Geometries and Theta-Relations

- Abstract: I will describe a conjectured identity between Siegel Theta-constants for special Riemann surfaces, and products of Jacobi theta-functions. This arises by comparing two different ways of computing the Renyi entropy of free fermions at finite temperature. For genus 2, the identity is a consequence of a result of Fay for branched Riemann surfaces. For general genus a proof is not yet available but I will indicate some evidence for the identity based on counting of zeroes.

◆ Sungjay Lee (KIAS)

- Title: Modular Constraints on (S)CFTs

14 TUE

◆ Alejandra Castro (UVA Amsterdam)

- Title: Holography and Siegel paramodular forms

- Abstract: I will discuss the application of Siegel paramodular forms to the counting of states in symmetric product orbifold CFTs. There are five special examples for which we provide exact analytic counting formulas for their polar states. The first example reproduces the known result for type IIB supergravity on AdS_3x S^3xK3, whereas the other four examples give new counting formulas. Their crucial feature is that the low energy pectrum is very sparse, which suggests the existence of a suitable dual supergravity theory. These examples open a path to novel realizations of AdS_3/CFT_2.

◆ Hidekazu Furusho (Nagoya)

- Title: On the coefficients of the Alekseev Torossian associator

- Abstract: In my talk I will explain a method to calculate the coefficients of the Alekseev-Torossian associator as linear combinations of iterated integrals of Kontsevich weight forms of Lie graphs.

◆ Albrecht Klemm (Bonn)

◆ Shamit Kachru (Stanford)

- Title: Black holes, class numbers, and special cycles

- Abstract:  I discuss a relationship between BPS black holes in string theory compactification on K3 x T2 and class numbers of binary quadratic forms with negative discriminant. This is a special example of a more general connection between results of Kudla-Millson concerning automorphy of special cycles in Shimura varieties and BPS state counts in string theory.

15 WED

◆ Yvonne Geyer (IAS Princeton)

- Title: QFT amplitudes from the Riemann Sphere

- Abstract: Massless Quantum Field Theories can be described perturbatively by chiral worldsheet models - the so-called Ambitwistor Strings. In contrast to conventional string theory, where loop amplitudes are calculated from higher genus Riemann surfaces, loop amplitudes in the ambitwistor string localise on the non-separating boundary of the moduli space. I will describe the resulting framework for QFT amplitudes from (nodal) Riemann spheres, building up from tree-level to two-loop amplitudes.

◆ Erik Panzer (Oxford)

◆ Lance Dixon (Stanford)

- Title: Co-action principle and amplitudes in planar N=4 super-Yang-Mills theory

- Abstract: The six-point amplitude in planar N=4 super-Yang-Mills theory, a function of three kinematical variables, can be computed through six loops by a bootstrap procedure. The amplitudes, when properly normalized, belong to a space of multiple polylogarithms called hexagon functions. Understanding the minimal space of such functions is key to being able to get to six loops. Importantly, the space satisfies a set of restrictions which correspond to a co-action principle of the type discussed by Schnetz, Brown, and Panzer. This is true both at the level of full functions, and also at the level of numbers that appear in specific limits, such as multiple-zeta values and Euler-Zagier sums. For a specific set of contributions called double pentaladder integrals, the co-action structure can be demonstrated to all loop orders, and even nonperturbatively, at finite coupling.

16 THU

◆ Philip Candelas (Oxford)

- Title: Periods of Calabi-Yau manifolds, zeta functions and attractor points

- Abstract: I will describe the process of computing the zeta functions for Calabi-Yau manifolds, and how we find nontrivial rank 2 attractor points from this data. If time allows, I will present preliminary results relating the values of the periods, for the values parameter corresponding to the attractor points, to values of the L-functions. This reports on joint work with Xenia de la Ossa, Mohamed Elmi and Duco van Straten.

◆ Jennifer Balakrishnan (Boston University)

- Title: Finding rational points on the split Cartan modular curve of level 13

- Abstract: We describe explicit aspects of arithmetic gauge theory and its role in the toolbox for understanding Diophantine questions. In particular, we discuss using the "quadratic" piece of the nonabelian Chabauty program to compute rational points on curves and outline a recent computation of rational points on the split Cartan modular curve of level 13, which is of interest due to a question of Serre on uniformity of residual Galois representations associated to elliptic curves. This is joint work with Netan Dogra, Steffen Mueller, Jan Tuitman, and Jan Vonk.

◆ David Broadhurst (Open University)

- Title: Eta quotients and Rademacher sums

- Abstract: Eta quotients on Gamma_0(6) yield evaluations of sunrise diagrams at 2, 3, 4 and 6 loops. At 2 and 3 loops, they provide modular parametrizations of inhomogeneous differential equations whose solutions are readily obtained by expanding in the nome. Atkin-Lehner transformations that permute cusps ensure fast convergence for all external momenta. At 4 and 6 loops, on-shell integrals are periods of modular forms of weights 4 and 6 given by Eichler integrals of eta quotients. Weakly holomorphic eta quotients determine quasi-periods. We give a Rademacher sum formula for Fourier coefficients of an eta quotient that is a Hauptmodul for Gamma_0(6) and generalize it for all levels with genus g = 0. There are elliptic obstructions at g = 1. We surmount these, showing how to handle all levels with genus g < 4 and examples with g = 4, 5, 6, 7, 8, 13. 

◆ Johannes Walcher (Heidelberg)

- Title: Arithmetics of A- and B-branes  

17 FRI

◆ Xenia de la Ossa (Oxford)

- Title: Moduli space of heterotic systems (or deformation theory of instanton connections on manifolds with certain G-structures)

◆ Meng-Chwan Tan (National University of Singapore)

- Title: From Little Strings to M5-branes via a Quasi-topological Sigma Model on Loop Group

- Abstarct: We unravel the ground states and left-excited states of the A_{k-1} N=(2,0) little string theory. Via a theorem by Atiyah, these sectors can be captured by a supersymmetric quasi-topological sigma model on CP^1 with target space the based loop group of SU(k). The ground states, described by L^2-cohomology classes, form modules over an affine Lie algebra, while the left-excited states, described by chiral differential operators, form modules over a toroidal Lie algebra. We also apply our results to unravel the 1/2 and 1/4 BPS sectors of the M5-brane worldvolume theory, which spectrum we find to be captured by cousins of modular and automorphic forms, respectively.

◆ Ingmar Saberi (Heidelberg)

- Title: Quasilocal fields on affine spaces over local fields

- Abstract: I'll give an overview, of a rough, imprecise, and speculative sort, of some models of scalar quantum field theory, defined on spacetimes which are affine, but over local fields other than the reals. Such models exhibit interesting uniformities across all places, and exhibit a discrete scale invariance which shows promise for physical applications: constructing discrete toy models of holography. It seems likely that similar models could be studied over local completions of function fields; this might be a promising way to think about constructing global versions of such models, whatever that might mean.

◆ Nima Arkani-Hamed (IAS Princeton)

- Title: Spacetime and Quantum Mechanics, Particles and Strings: Adventures in Combinatorial Positive Geometry at Infinity.