| Program&Abstract | Home > Program&Abstract |

Jihoon Lee
- Title: On the Blow-up and local well-posedness for the solutions to some axisymmetric inviscid Hall-MHD equations
- Abstract: In this talk, we consider the regularity problem of the solutions to the axisymmetric, inviscid and incompressible Hall-magnetohydrodynamics(Hall-MHD) equations.
First, we obtain the blow-up criterion for the axisymmetric resistive and inviscid Hall-MHD equations for the inviscid fluids. Second, we obtain the local-in-time existence of sufficiently regular solutions to the axisymmetric inviscid Hall-MHD equations without resistivity. Finally, we consider the inviscid axisymmetric Hall equations without fluids, and prove that there exists a finite time blow-up of a classical solution due to the Hall term. This is the joint work with Eunji Jeong(CAU) and Junha Kim(CAU).
Hisashi Okamoto
- Title: Existence proof of unimodal solutions via interval analysis
- Abstract: In this talk I consider the following equation:
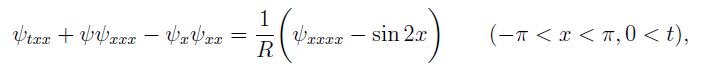
where ![]() is the unknown, the subscripts imply the differentiation, R is a positive parameter called the Reynolds number. This equation was derived by Proudman and Johnson [5] and I call it the Proudman--Johnson equation. Their original motive was to study a boundary layer of incompressible fluid motion but the equation is now used for many other purposes. See for instance [1].
is the unknown, the subscripts imply the differentiation, R is a positive parameter called the Reynolds number. This equation was derived by Proudman and Johnson [5] and I call it the Proudman--Johnson equation. Their original motive was to study a boundary layer of incompressible fluid motion but the equation is now used for many other purposes. See for instance [1].
Steady-states of the Proudman--Johnson equation are computed and they are proved rigorously to be unimodal via the interval arithmetic.
This is a joint work with Tomoyuki Miyaji of Meiji University.
[1] H. Bae, D. Chae, and H. Okamoto, On the well-posedness of various one-dimensional model equations for fluid motion, Nonlinear Analysis, 160, (2017), 25--43.
[5] I. Proudman and K. Johnson, Boundary-layer growth near a rear stagnation point, J. Fluid Mech., 12 (1962), 161--168.
Hantaek Bae
- Title: Regularity and decay properties of the incompressible Navier-Stokes equations
- Abstract: In this talk, I will consider the incompressible Navier-Stokes equations in the mild solution setting. Using this setting, I will show how to obtain analyticity of mild solutions using the Gevrey regularity technique. This regularity enables to get decay rates of weak solutions of the Navier-Stokes equations. This idea can be applied to other dissipative equations with analytic nonlinearities such as the inhomogeneous Navier-Stokes equations and the dissipative quasi-geostrophic equations.
Seungsu Hwang
- Title: Point vortices on the hyperbolic sphere
- Abstract: We will talk about dynamics of point vortices on a hyperbolic sphere with constant negative curvature. After discussing possible motions including equilibria and collisions, relative equilibria of point vortices on a hyperbolic sphere with constant negative curvature is formulated and considered
Hyunseok Kim
- Title: On weak and very weak solutions of the stationary Navier-Stokes equations
- Abstract: The purpose of this talk is to study to the stationary Navier-Stokes equations in a bounded or exterior domain Ω in R^3.
After briefly explaining the classical theory of weak solutions due to Jean Leray (1933), we will introduce the concept of very weak solutions and present some recent results on existence, uniqueness, and regularity for very weak solutions.
Robert Krasny
- Title: A New Implementation of the Vortex Method for Incompressible Fluid Flow
- Abstract: We discuss a new implementation of the vortex method for the incompressible Euler equations. This work focuses on smooth vorticity distributions as opposed to vortex sheets. As usual the vorticity is carried by Lagrangian particles and the velocity is recovered by the Biot-Savart law. The new implementation combines remeshing, adaptive refinement, and treecode acceleration to resolve complex features of the flow. Applications are given to tracer transport and vortex dynamics on a rotating sphere, and to vortex dynamics in two-dimensional free-space. This is joint work with Ling Xu and Peter Bosler.
Kyudong Choi
- Title: 1D Models of 2D Inviscid Boussinesq System
- Abstract: In connection with the recent proposal for possible singularity formation at the boundary for solutions of three-dimensional axisymmetric incompressible Eu-ler’s equations (Luo and Hou, Proc. Natl. Acad. Sci. USA (2014)), we study models for the dynamics at the boundary and show that they exhibit a finite-time blowup from smooth data.
Moon-Jin Kang
- Title: Contraction for large perturbation of shocks of barotropic Navier-Stokes system
- Abstract:In this talk, I present a proof on contraction property for any weak perturbations of viscous shocks of the barotropic Navier-Stokes system, by constructing a weighted relative entropy and time-dependent shift. The contraction property of the shocks does not depend on the viscosity coefficient. Therefore, this provides a weak compactness for the inviscid limit problem, that is, entropy shocks for the isentropic Euler system are stable and unique in the class of weak inviscid limits of solutions to the Navier-Stokes system. This result becomes an important cornerstone in the study for the long standing conjecture on uniqueness of entropy weak solutions as follows:
The compressible Euler equations admit a unique entropy weak solution in a class of vanishing viscosity solutions as inviscid limits of solutions to the associated viscous system that is compressible Navier-Stokes system
